Quantum LMSR: Accelerating String Rotation

Mark Boady & Gary Pham College of Computing & Informatics Drexel University
QR Code Scan for References Click here to go to website

Research Motivation

  • Many benzenoid hydrocarbons admit multiple boundary-edge codes under different rotations of their outer face.
  • These codes depend on the chosen start vertex (commonly the lowest-left) and the traversal direction.
  • A single canonical code per isomorphism class enables fast equality checks and compact chemical indexing.
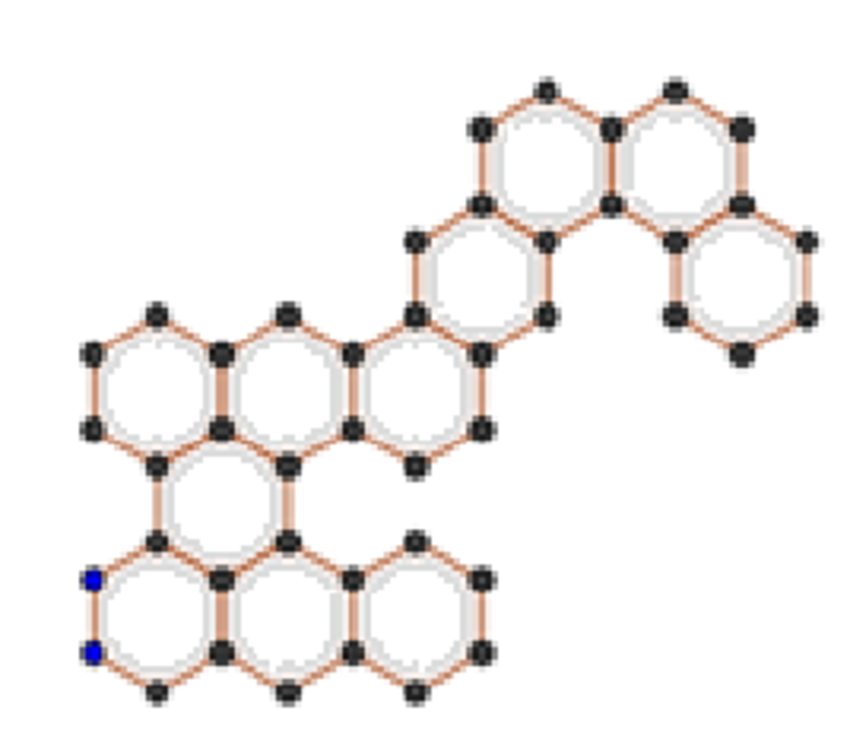
    • Benzenoid

    Fig 1: Original Compound

    Benzenoid

    Fig 2: Rotated Compound

Classical Approach

  • Traverse the outer face of the molecular graph, recording turn-and-edge types into a sequence.
  • Generate all cyclic shifts of this boundary-edge code (string rotations) to capture every possible "view".
  • Use a minimal-rotation algorithm (e.g., Booth's or Duval's) to pick the lexicographically smallest string rotation (LMSR).

Computational Problem

  • Given a boundary-edge code of length \(n\), find its minimal cyclic rotation (the canonical form).
  • Best classical complexity: \(O(n)\) or \(O(n \log n)\) for minimal-rotation string algorithms.
  • Quantum proposal: employ QRAM to load all rotations in superposition and use Grover-style search over indices for a potential speed-up.
    • Qubit Representation

    Fig 3: Bit vs Qubit

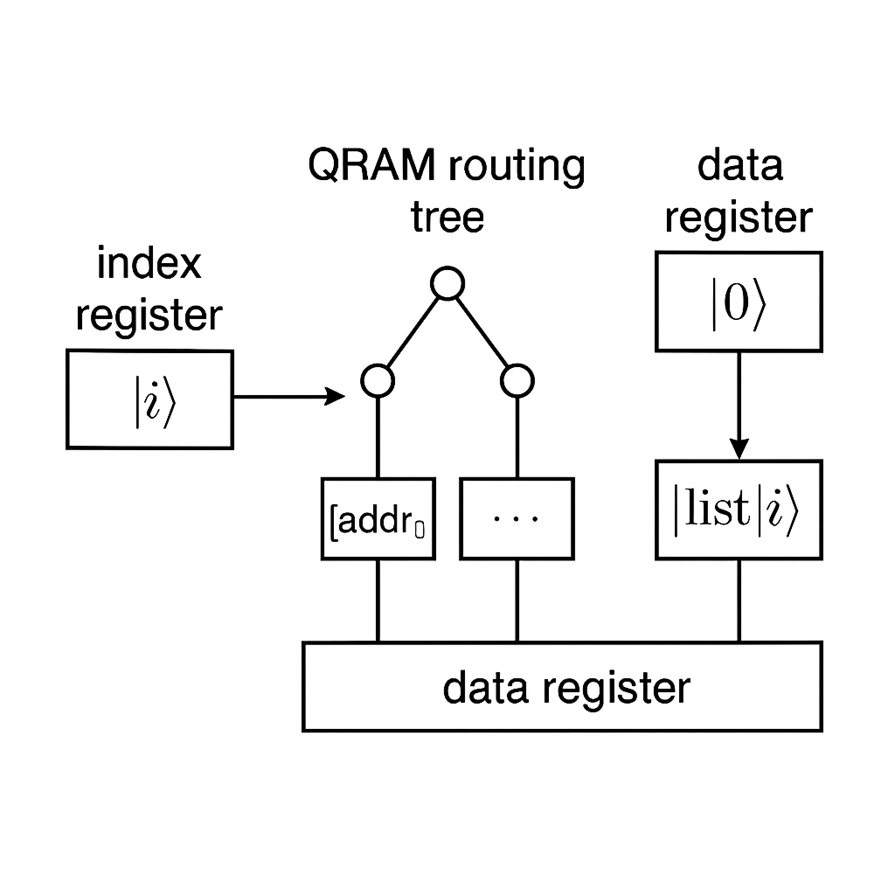
    QRAM Architecture

    Fig 4: QRAM

Quantum Lists & Superposed Indexing

  • What is a Quantum List?
    • A mapping between an index and a data register via QRAM:
    • \(\sum_i a_i \lvert i\rangle \otimes \lvert 0\rangle \xrightarrow{\text{QRAM}} \sum_i a_i \lvert i\rangle \otimes \lvert \text{list}[i]\rangle\)
    • Effectively loads all list entries into superposition at once
  • Key Properties:
    • Read-only: preserves no-cloning (query without destructive overwrite)
    • Parallel lookup: one QRAM query accesses every element weighted by its amplitude
    • Unitary & reversible: routing and fan-out built entirely from reversible gates
  • Our Proposal: superpose the index register itself to enable end-to-end quantum parallelism

Quantum Approach

  • Use Grover's search to locate minimal rotation index with \(O(\sqrt{n})\) queries.
  • Encode rotation cost function as quantum oracle: \[O_f:\lvert i\rangle\lvert0\rangle \to \lvert i\rangle(-1)^{f(i)}\lvert0\rangle.\]
  • Amplitude amplification finds marked index faster than classical scan.
  • Key Components:
    • Phase oracle: Marks minimal rotation indices
    • Diffusion operator: Inverts amplitudes about mean
    • Superposition enables parallel evaluation
    • Quantum parallelism: \(O(n) \to O(\sqrt{n})\)

Algorithm Steps

  • Initialize a loop over rotation indices
  • Within each iteration:
    • Step 1: Find the current minimum via the marked-state oracle (Dür & Høyer)
    • Step 2: Prepare the oracle, diffusion operator, and inc_modM gate (\(M\) = list length)
    • Step 3: Execute Grover search for \(k\) iterations
    • Step 4: Measure the quantum register
    • Step 5: Check stopping criteria; if not met, continue
  • After exiting the loop, retrieve the minimal-rotation index, undo any modular increments, and return it

Visualization & Results

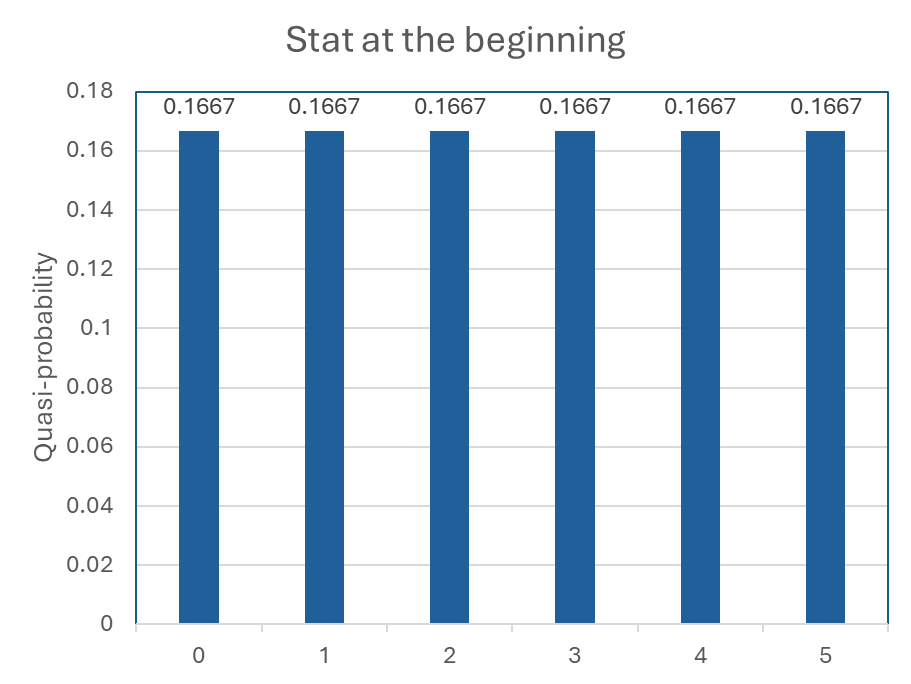
Algorithm Visualization 1

Fig 5: Initial state with uniform superposition

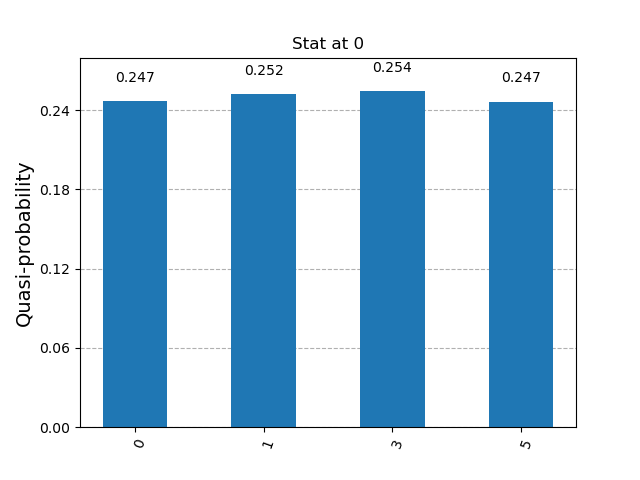
Algorithm Visualization 2

Fig 6: First iteration result

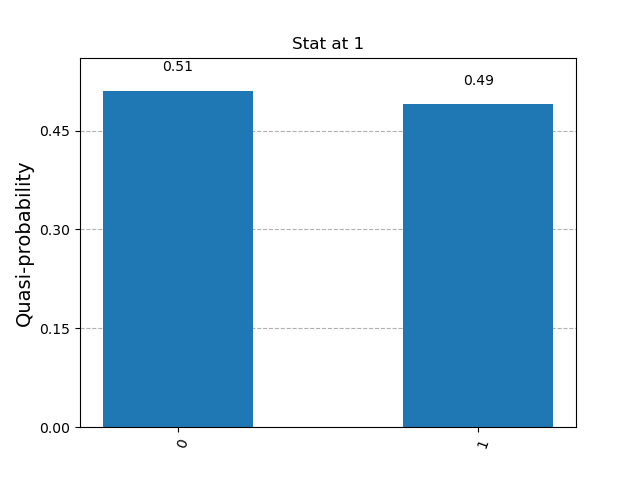
Algorithm Visualization 3

Fig 7: Second iteration result

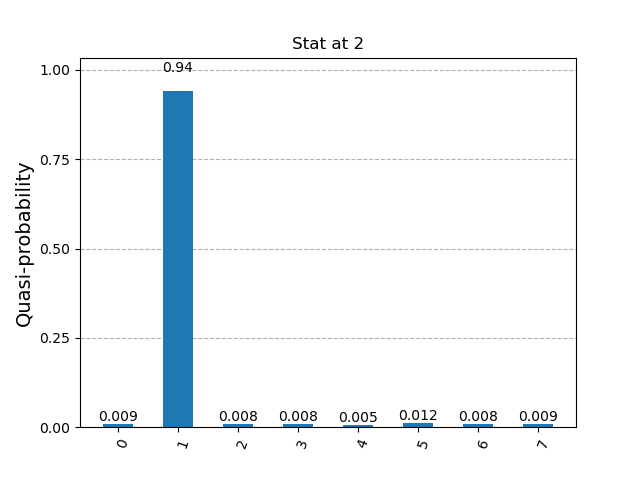
Algorithm Visualization 4

Fig 8: Last iteration result & measurement outcome

Circuit Structure

  • Apply Hadamard gates to all index qubits to create superposition
  • Perform \(\lfloor(\pi/4)\cdot\sqrt{N/M}\rfloor\) Grover iterations per loop:
    • Oracle marks the current minimum rotation index
    • Diffusion operator amplifies marked amplitude
    • inc_modM gate increments indices modulo \(M\)
  • Measure the index register each iteration and check stopping criteria
  • Once done, uncompute any modular increments and output the minimal-rotation index
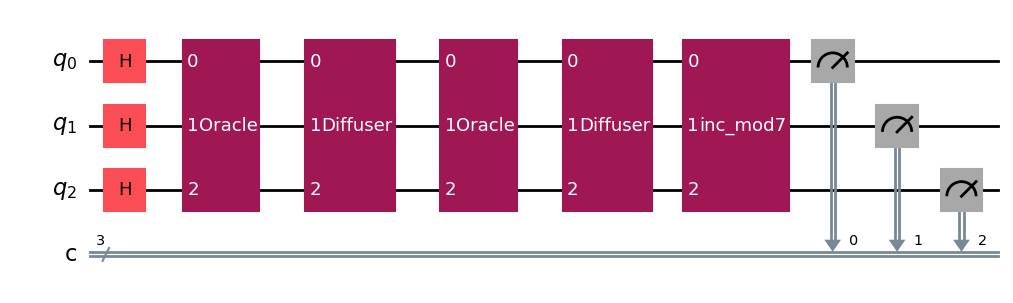
Grover Circuit

Fig 9: Grover's Algorithm Circuit

Complexity & Resource Analysis

Comparator Average Worst Qubit Usage
Booth's Algorithm \(\Theta(n)\) \(\Theta(n)\) \(n\) classical bits
Proposed (no QRAM) \(\Theta(n)\) \(\Theta(n^2)\) \(\Theta(\log n)\)
Published LMSR \(\Theta(n^{3/4})\) \(\Theta(\sqrt{n}\log n)\) \(\Theta((\log n)^2)\)
Proposed + QRAM (binary search) \(\Theta(\sqrt{n}\log n)\) \(\Theta(\sqrt{n}\log n)\) \(n + \Theta(\log n)\)
Proposed + QRAM (hashing) \(\Theta(\sqrt{n})\) \(\Theta(\sqrt{n}\log n)\) \(n + \Theta(\log n)\)
Scaling Plot

Fig 10: Performance Scaling Analysis

Key Takeaways

  • Rotation as a Unifier: Across strings, molecules, and quantum data, rotations preserve core structure while offering new "views" for canonicalization.
  • Quantum Enhancement: QRAM + superposed indexing unlocks massive parallelism, enabling rotation-based searches on quantum hardware.
  • Benzenoid Canonicalization: Lexicographically minimal rotations of boundary-edge codes yield unique, compact molecular identifiers for chemical databases.

Conclusion

  • Impact & Applications: Chemical Informatics, Pattern Matching, Foundation for broader quantum data structures.
  • Future Work: 3D & Dihedral Symmetries, Robust QRAM Architectures, Integration with Quantum Circuits
  • Architecture: QRAM enables parallel string rotation access with \(O(\sqrt{n})\) speedup.